ตัวอย่าง Cosine Distance ระหว่าง 1-D arrays หรือระหว่าง Vector แต่ละคู่

บทความโดย ผศ.ดร.ณัฐโชติ พรหมฤทธิ์
ภาควิชาคอมพิวเตอร์
คณะวิทยาศาสตร์
มหาวิทยาลัยศิลปากร

Cosine Distance คือค่าที่ใช้วัดความไม่คล้ายกันระหว่างเวกเตอร์สองตัวในพื้นที่เวกเตอร์โดยใช้ Cosine Similarity ในการคำนวณความไม่คล้ายกัน (Dissimilarity) ซึ่งมีสูตรดังนี้:

Cosine Similarity = A⋅B/∥A∥∥B∥

A⋅B คือ dot product ระหว่างเวกเตอร์ A และ B
∥A∥ คือความยาว (magnitude) ของเวกเตอร์ A
∥B∥ คือความยาว (magnitude) ของเวกเตอร์ B

Cosine Distance=1−Cosine Similarity

ให้เวกเตอร์ A=[1,2,3] และ B=[4,5,6]

คำนวณ Dot Product
A⋅B=1∗4+2∗5+3∗6=4+10+18=32

คำนวณ Magnitude ของเวกเตอร์ A
∥A∥=sqrt(1^2+2^2+3^2​=sqrt(1+4+9​)=sqrt(14)

คำนวณ Magnitude ของเวกเตอร์ B
∥B∥=sqrt(4^2+5^2+6^2)​=sqrt(16+25+36)​=sqrt(77​)

คำนวณ Cosine Similarity
Cosine Similarity=32/sqrt(14)*​sqrt(77)≈0.9746

การคำนวณ Cosine Distance
Cosine Distance=1−0.9746≈0.0254

import plotly.express as px
from nltk.cluster.util import cosine_distance

cosine_distance([1,2,3], [4,5,6])

0.025368153802923787

fig = px.scatter(x=[3, 3, 0, 2], y=[14, 0, 16, 0])
fig.add_shape(type='line', x0=0, y0=0, x1=0, y1=16, line=dict(color='Red'))
fig.add_shape(type='line', x0=0, y0=0, x1=3, y1=14, line=dict(color='Red'))
fig.add_shape(type='line', x0=0, y0=0, x1=3, y1=0, line=dict(color='Red'))

fig.update_layout(
    yaxis=dict(scaleanchor="x", scaleratio=1),
    xaxis=dict(constrain="domain"),
    width=800,  
    height=600
)

fig.show()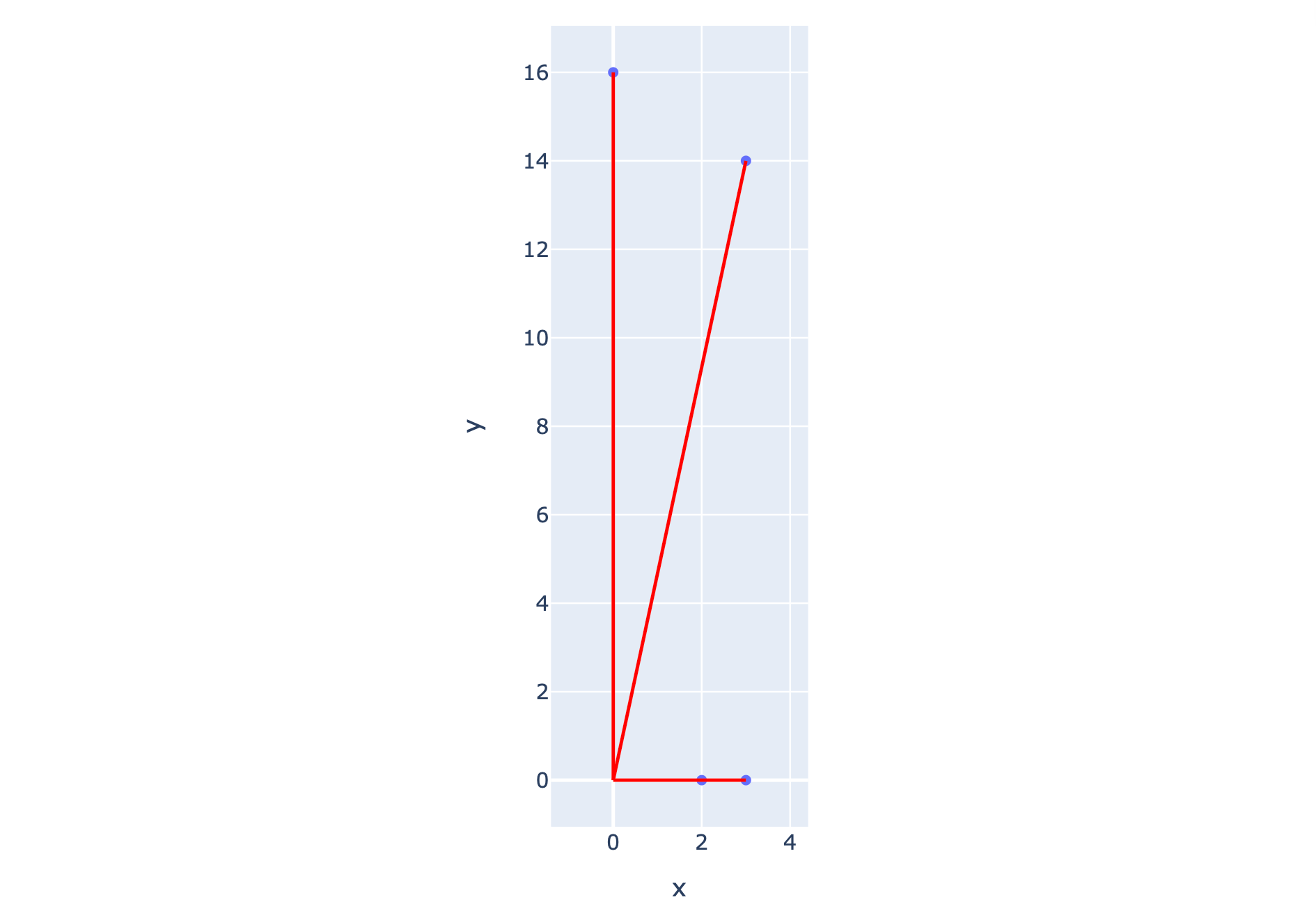

cosine_distance([0,16], [3,14])

0.02219758592259058

cosine_distance([3,14], [3,0])

0.7904709112691265

cosine_distance([3,14], [2,0])

0.7904709112691266

cosine_distance([0,16], [2,0])

1.0

cosine_distance([0,16], [3,0])

1.0